leetcode之树 easy部分

发表于

记录在算法学习过程中与树相关的题目,easy部分。

938 Range Sum of BST

题目描述

Given the root node of a binary search tree, return the sum of values of all nodes with value between L and R (inclusive).
The binary search tree is guaranteed to have unique values.

题目解析

给定一个二叉搜索树，L和R，返回节点值在L和R的所有节点值之和。
递归遍历，累加在给定范围内的节点的值。因为是二叉搜索树，所以在遍历时可以根据父节点的值决定下一步遍历左子树还是右子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int sum;
    int rangeSumBST(TreeNode* root, int L, int R) {
        sum = 0;
        helper(root,L,R);
        return sum;   
    }

    void helper(TreeNode* root, int L, int R){
        if(!root)
            return;
        if(root->val >= L && root->val <= R){
            sum += root->val;
        }
        if(root->val > L){
            helper(root->left,L,R);
        }
        if(root->val < R){
            helper(root->right,L,R);
        }
        return;
    }   
};

617 Merge Two Binary Trees

题目描述

Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.

You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.

题目解析

合并两个二叉树，对于重合节点则是节点值相加，未重合节点作为合并后的树的新的节点。
递归合并，当有重合节点时节点值为原来两个二叉树节点值的加和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        if(!t1 && !t2)
            return NULL;
        if(!t1 && t2)
            return t2;
        if(t1 && !t2)
            return t1;
        TreeNode *t = new TreeNode(t1->val + t2->val);
        t->left = mergeTrees(t1->left,t2->left);
        t->right = mergeTrees(t1->right,t2->right);
        return t;
    }
};

700 Search in a Binary Search Tree

题目描述

Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node’s value equals the given value. Return the subtree rooted with that node. If such node doesn’t exist, you should return NULL.

题目解析

二叉搜索树，对于给定值，在二叉搜索树种找到该节点并返回。
利用二叉搜索树的根节点数值大于它的左子树节点数值，小于它的右子树节点数值。先判断根节点与给定val的大小，若相等则直接返回，若大于根节点，则在右子树种继续寻找，反之则在左子树种寻找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(!root)
            return NULL;
        if(root->val == val)
            return root;
        
        if(root->val > val)
            return searchBST(root->left, val);
        else
            return searchBST(root->right, val);
    }
};

看到一个执行效率更快的答案，同样是递归，但是作者在代码中关闭了iostream的输入缓存，因此执行效率更快，还有这种操作！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
// Live coding problems, watch at
// https://www.twitch.tv/yipcubed
// https://www.youtube.com/channel/UCTV_UOPu7EWXvYWsBFxMsSA/videos
//

// makes code faster, but larger. Just for LeetCode fun!
#pragma GCC optimise ("Ofast")

// makes stdin not synced so it is faster. Just for LeetCode fun!
static auto _no_sync_ __attribute__((unused)) = []() {              // NOLINT
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    return nullptr;
}();

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (!root) return nullptr;
        if (root->val == val)
            return root;
        if (val < root->val)
            return searchBST(root->left, val);
        else
            return searchBST(root->right, val);

    }
};


# 589 N-ary Tree Preorder Traversal
## 题目描述
Given an n-ary tree, return the preorder traversal of its nodes' values.

## 题目解析
树的前序遍历，递归遍历，左孩子->父节点->右孩子
~~~c++
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> ans;
    vector<int> preorder(Node* root) {
        if(!root)
            return ans;
        ans.push_back(root->val);
        vector<Node*> _children = root->children;
        for(int i=0;i<_children.size();i++){
            preorder(_children[i]);
        }
        return ans;
        
    }
};

590 N-ary Tree Postorder Traversal

题目描述

Given an n-ary tree, return the postorder traversal of its nodes’ values.

题目解析

树的后序遍历，左孩子->右孩子->父节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> ans;
    vector<int> postorder(Node* root) {
        if(!root)
            return ans;
        vector<Node*> _children = root->children;
        for(int i=0;i<_children.size();i++){
            //ans.push_back(_children[i]->val);
            postorder(_children[i]);
        }
        ans.push_back(root->val);
        return ans;
    }
};

965 Univalued Binary Tree

题目描述

A binary tree is univalued if every node in the tree has the same value.

Return true if and only if the given tree is univalued.

题目解析

判断是否为单值树，以根节点的值为比较值，先比较左子树，再比较右子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        if(!root)
            return true;
        int ans = root->val;
        if(_isUnivalTree(root->left,ans))
            return _isUnivalTree(root->right,ans);
        else
            return false;


    }

    bool _isUnivalTree(TreeNode* root, int _val){
        if(!root)
            return true;
        if(root->val == _val){
            if(_isUnivalTree(root->left,_val))
                return _isUnivalTree(root->right,_val);
            else
                return false;

        }
        else
            return false;
    }
};

559 Maximum Depth of N-ary Tree

题目描述

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

题目解析

求多叉树的深度，递归每次遍历孩子节点时取最大深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    
    int maxDepth(Node* root) {
        if(!root)
            return 0;
        vector<Node*> _children = root->children;
        vector<int> depth;
        for(int i=0;i<_children.size();i++){
            depth.push_back(maxDepth(_children[i]));
        }
        int ans = 0;
        for(int i=0;i<depth.size();i++)
            if(ans < depth[i])
                ans = depth[i];
        return (ans+1);
    }
};

897 Increasing Order Search Tree

题目描述

Given a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only 1 right child.

题目解析

给定二叉搜索树，以最左边节点为根，重新排列子树，最后的树只有右子树，没有左子树
思路：重新建立一个BST，newRoot赋值为0，递归遍历左子树，将newRoot的左子树赋值为root->val，因为遍历是递归遍历，所以赋值顺序是从原来BST的左孩子节点到根节点，左子树递归完成后root也被赋值了，然后再遍历右子树。最后返回的是newRoot的右子树。这里用到一个临时节点，因为每次都只赋值给新BST的右孩子。
注意：每次赋值给新BST只需要原来BST的节点值即可，不能将节点赋值给新的BST

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* newRoot = new TreeNode(0);
    TreeNode* temp = newRoot;
    TreeNode* increasingBST(TreeNode* root) {
        if(!root)
            return NULL;
        if(root->left)
            increasingBST(root->left);
        temp->right = new TreeNode(root->val);
        temp = temp->right;
        if(root->right)
            increasingBST(root->right);
        return newRoot->right;
    }
};

872 Leaf-Similar Trees

题目描述

Consider all the leaves of a binary tree. From left to right order, the values of those leaves form a leaf value sequence.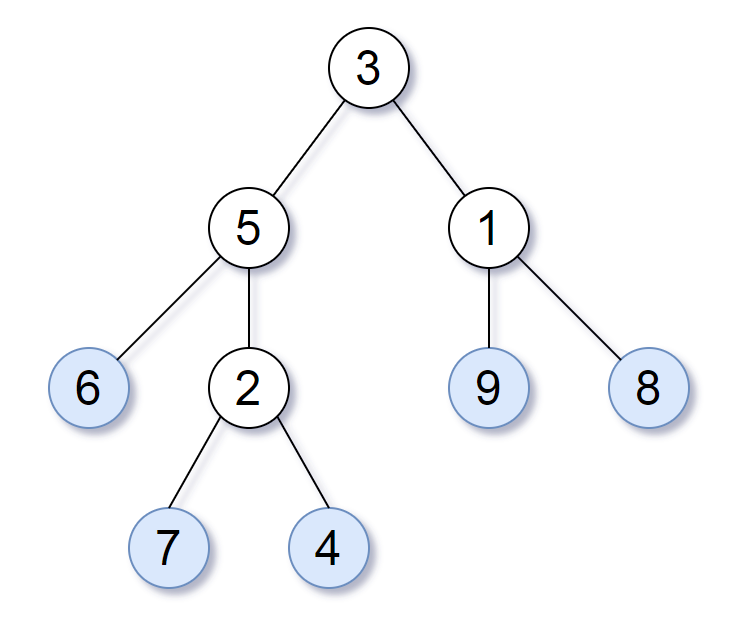
1
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

题目解析

求二叉树的叶值序列，若两个二叉树的叶值序列是相似的，则它们是leaf-similar。
思路是求每一个二叉树的叶值序列，然后比较两个序列，注意的是递归的传参，最好不要在参与递归的函数里定义在递归过程中会变化的变量，可以让他们作为参数传进去。另外就是注意二叉树为空的判断。vector的变量可以直接用运算符比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool leafSimilar(TreeNode* root1, TreeNode* root2) {
        if(!root1 && !root2)
            return true;
        if((!root1 && root2)||(root1 && !root2))
            return false;
        vector<int> s1,s2;
        leafSequence(s1,root1);
        leafSequence(s2,root2);

        if(s1 == s2)
            return true;
        else
            return false;
    }

    void leafSequence(vector<int> &ans, TreeNode* root){
        if(root->left==NULL && root->right==NULL){
            ans.push_back(root->val);
            return;
        }
        else{
            if(root->left)
                leafSequence(ans,root->left);
            if(root->right)
                leafSequence(ans,root->right);
        }
    }
};

104 Maximum Depth of Binary Tree

题目描述

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

题目解析

求二叉树的最大深度
之前做过求多叉树的深度(559 Maximum Depth of N-ary Tree)，分别递归求左子树和右子树的深度，返回它们最大值+1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root)
            return 0;
        int leftDepth=0,rightDepth=0;
        leftDepth = maxDepth(root->left);
        rightDepth = maxDepth(root->right);

        return(max(leftDepth,rightDepth)+1);
    }
};

因为这些题目是之前做的，现在想系统的整理一下，没有记录参考链接，以后的题目一定记录，感谢给予帮助的各位大佬们~~

669 Trim a Binary Search Tree

题目描述

Given a binary search tree and the lowest and highest boundaries as L and R, trim the tree so that all its elements lies in [L, R] (R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.

题目解析

二叉树的修剪，给定L和R，如果树的节点值不在[L,R]区间内，就要进行剪枝。因为给定的是一个二叉搜索树，所以它的父节点值一定大于左子树的节点值，且小于其右子树的节点值。递归修剪，如果root为空，直接返回；如果root的节点值大于R，那么符合[L,R]的节点只可能在其左子树中；如果root的节点值小于L，那么在[L,R]中的节点只可能在其右子树中；如果root的节点值在[L,R]之间，则其左子树和右子树需要继续递归修剪。
对递归了解的不深入，总的思想明白，但是不会写代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int L, int R){
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        if(!root)
            return NULL;
        if(root->val < L)
            return trimBST(root->right,L,R);
        if(root->val > R)
            return trimBST(root->left,L,R);
        else{
            root->left = trimBST(root->left,L,R);
            root->right = trimBST(root->right,L,R);
            return root;
        }
    }
};

参考

https://www.jianshu.com/p/2210542fb2ed

429 N-ary Tree Level Order Traversal

题目描述

Given an n-ary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).

题目解析

给定多叉树，分层遍历，返回其节点值。
开始写算法的时候不知道怎么先把根节点的值保存，因为使用的是递归，因此如果是仅仅简单的使用一个push_back(root)，就会把每个非叶子节点都单独的push_back一次，看了一个参考的答案，它是利用一个变量来保存树的层数，当res的size比树的层数小时，会对res进行resize，然后再遍历其孩子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<vector<int>> levelOrder(Node* root){
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        vector<vector<int>> res;
        helper(root,0,res);
        return res;
    }
    void helper(Node* root,int level, vector<vector<int>>& res){
        if(!root)
            return;
        if(res.size()<=level)
            res.resize(res.size()+1);
        res[level].push_back(root->val);
        for(auto node : root->children)
            helper(node,level+1,res);
    }
};

参考里还有迭代遍历的算法。

参考

https://www.cnblogs.com/grandyang/p/9672233.html

1022 Sum of Root To Leaf Binary Numbers

题目描述

Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

For all leaves in the tree, consider the numbers represented by the path from the root to that leaf.

Return the sum of these numbers.

题目解析

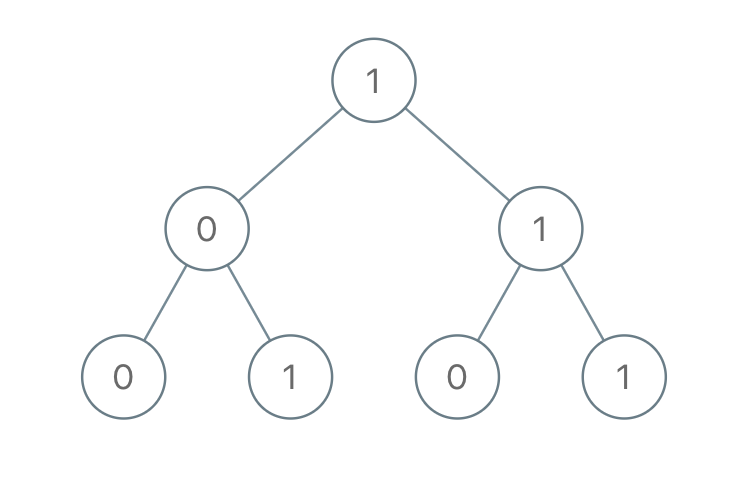
给定一个二叉树，每个节点的值是0或1，每个从根到叶的路径代表一个从最高有效位开始的二进制数，返回树中所有路径的二进制数之和。例如下面一颗二叉树，它的路径有100,101,110,111。与以往的遍历不一样，每一个非叶子节点的值需要用到多次，我开始的方式当切换到另外一颗子树时，前面左子树的值还在临时变量中，这就导致多加了一个节点值，临时变量我是用vector来存储的，每次遇到叶子结点就pop_back一次，当计算第三条路径110时，跟节点的左子树的节点值就还在容器里。贴上我未成功的答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> res_bin;
    int ans = 0;
    int sumRootToLeaf(TreeNode* root) {
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        helper(root);
        return ans;
    }
    void helper(TreeNode* node){
        if(!node){
            return;
        }
        res_bin.push_back(root->val);
        if(!root->left && !root->right){
            ans += Bin2Dec(res);
            res_bin.pop_back();
        }
        else{
            helper(node->left);
            helper(node->right);
        }
    }
    int Bin2Dec(vector<int> m){
        int sum = 0;
        for(int i=m.size()-1,int j=0;i>=0;i--,j++){
            sum = sum + m[i] * pow(2,j);
        }
        return sum;

    }
};

后来我是看了参考的链接，解法中二进制转十进制的方法很巧妙，原来的val左移一位再加上当前节点值。这里使用一个临时变量newVal，因为它每次都会重新定义和赋值，而且val左移一位只会影响newVal的值，不会影响自身的值，当是叶子节点时，就累加，然后递归左子树，再递归右子树，这里右子树使用的newVal不受左子树中newVal的影响，这也是我的代码计算错误的原因，可以在调试时输出每次val和newVal的值看一下。

1
int newVal = val << 1 | (node->val);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    //vector<int> res_bin;
    int ans = 0;
    int sumRootToLeaf(TreeNode* root) {
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        helper(root, 0);
        return ans;
    }
    void helper(TreeNode* node, int val){
        if(!node)
            return;
        int newVal = val << 1 | (node->val);
        if(!node->left && !node->right){
            ans += newVal;
        }
        else{
            helper(node->left,newVal);
            helper(node->right,newVal);
        }
    }
};

2

参考

https://leetcode-cn.com/problems/sum-of-root-to-leaf-binary-numbers/solution/dfswei-yun-suan-jian-dan-gao-xiao-by-w1sl1y/

226 Invert Binary Tree

题目描述

Invert a binary tree.
Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input:

     4
   /   \
  2     7
 / \   / \
1   3 6   9
Output:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

题目解析

二叉树的镜像翻转，一直在纠结递归函数返回值的问题。中间的是可以不要返回值，最后返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root)
            return NULL;
        if(root->left || root->right){
            TreeNode *node;
            node = root->right;
            root->right = root->left;
            root->left = node;
            invertTree(root->left);
            invertTree(root->right);
        }
        
        return root;
    }
};

637 Average of Levels in Binary Tree

题目描述

Given a non-empty binary tree, return the average value of the nodes on each level in the form of an array.
Example 1:

1
2
3
4
5
6
7
Input:
    3
   / \
  9  20
    /  \
   15   7
Output: [3, 14.5, 11]

Explanation:
The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].

题目解析

二叉树的层次遍历，求二叉树每层的所有节点的平均值。解法和之前做过的多叉树的层次遍历类似。先遍历保存每层节点，再计算平均值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>> vals;
    vector<double> averageOfLevels(TreeNode* root) {
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);

        helper(root,0);

        vector<double> ans(vals.size(),0.0);
        int i,j;
        for(i=0;i<vals.size();i++){
            for(j=0;j<vals[i].size();j++)
                ans[i] += vals[i][j];
            ans[i] /= vals[i].size();
        }

        return ans;
    }

    void helper(TreeNode* root, int level){
        if(!root)
            return;
        if(vals.size()<=level)
            vals.resize(vals.size()+1);
        vals[level].push_back(root->val);
        helper(root->left,level+1);
        helper(root->right,level+1);
    }
};

653 Two Sum IV - Input is a BST

题目描述

Given a Binary Search Tree and a target number, return true if there exist two elements in the BST such that their sum is equal to the given target.

题目解析

给定一个数值，如果二叉树中有两个节点之和等于给定数值，则返回true，否则返回false。注意节点值有可能是负数。开始我是判断了节点值与target的关系，如果节点值大于等于该target，就只遍历左子树了，但是现在有负数存在，所以都要遍历，原来存储的vector也变成了map。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    map<int,int> m;
    bool findTarget(TreeNode* root, int k) {
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        
        helper(root,k);
        map<int,int>::iterator iter;
        for(iter=m.begin();iter!=m.end();iter++){
            if(m[iter->first] && iter->first != k-iter->first){
                if(m[k-iter->first]==1)
                    return true;   
            }
        }
        return false;
    }
    void helper(TreeNode* root, int k){
        if(!root)
            return;
        m[root->val] = 1;
        helper(root->left,k);
        helper(root->right,k);
    }
};

优化

108 Convert Sorted Array to Binary Search Tree

题目描述

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

1
2
3
4
5
6
7
8
9
Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

题目解析

将一个有序数组转化为二叉搜索树，而且二叉树必须是高度平衡的，也就是说构造的二叉搜索树中每个节点的两个子树的深度相差不超过1。以数组中的中位数为根节点，中位数左边的子集用来构建左子树，中位数右边的子集用来构造右子树。注意边界的判断，left和right相等时表示只有一个元素了，直接new返回返回，正常情况下是left < right。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if(!nums.size())
            return NULL;
        return helper(nums,0,nums.size()-1);
    }
    
    TreeNode* helper(vector<int> &nums,int left, int right){
        if(left > right)
            return NULL;
        if(left == right)
            return new TreeNode(nums[left]);
        int mid = (left + right) / 2;
        TreeNode *root = new TreeNode(nums[mid]);
        root->left = helper(nums,left,mid-1);
        root->right = helper(nums,mid+1,right);
        return root; 
    }
};

参考

https://leetcode.com/problems/convert-sorted-array-to-binary-search-tree/discuss/401863/Simple-Recursion-based-C%2B%2B-code.-Faster-than-98.

538 Convert BST to Greater Tree

题目描述

Given a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus sum of all keys greater than the original key in BST.

Example:

1
2
3
4
5
6
7
8
9
Input: The root of a Binary Search Tree like this:
              5
            /   \
           2     13

Output: The root of a Greater Tree like this:
             18
            /   \
          20     13

题目解析

题目要求将树的每个节点与比这个节点大的所有节点值相加，变成一棵更大的树。因为是二叉搜索树，所以中序遍历正好是从小到大排序，我先采用中序遍历将所有的值保存在一个数组中，然后求和为sum。再进行一次中序遍历，在中序遍历时不断的递减这个sum，然后与当前节点值相加。其实我这样有点绕，每次的sum值就是需要的当前节点的节点值，另外也不需要将节点值都保存下来，因为最后只需要一个和，但是我将push_back改为累加后，runtime的时间居然更大了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> v;
    int sum;
    TreeNode* convertBST(TreeNode* root) {
        if(!root)
            return NULL;
        helper(root);
        sum = accumulate(v.begin(),v.end(),0);
        addBST(root);
        return root;
    }

    void helper(TreeNode* root){
        if(!root)
            return;
        helper(root->left);
        v.push_back(root->val);
        helper(root->right);
        return;
    }
    void addBST(TreeNode* root){
        if(!root)
            return;
        addBST(root->left);
        sum -= root->val;
        root->val += sum;
        addBST(root->right);
        return;
    }
};

优化

看到一个比较好理解的答案，是按照右子树、根节点、左子树的顺序遍历，同时用sum累加保存节点值，并与当前root->val进行相加。这样正好利用了BST的特点，遍历的节点顺序正好是从大到小的顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        int sum = 0;
        convertBST(root, sum);
        return root;
    }
    
    void convertBST(TreeNode* root, int &sum) {
    	if(root==NULL) return;
    	convertBST(root->right, sum);
    	root->val = root->val + sum;
    	sum = root->val;
    	convertBST(root->left, sum);
    }
};

606 Construct String from Binary Tree

题目描述

You need to construct a string consists of parenthesis and integers from a binary tree with the preorder traversing way.

The null node needs to be represented by empty parenthesis pair “()”. And you need to omit all the empty parenthesis pairs that don’t affect the one-to-one mapping relationship between the string and the original binary tree.
Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
Input: Binary tree: [1,2,3,4]
       1
     /   \
    2     3
   /    
  4     

Output: "1(2(4))(3)"

Explanation: Originallay it needs to be "1(2(4)())(3()())", 
but you need to omit all the unnecessary empty parenthesis pairs. 
And it will be "1(2(4))(3)".

Example 2:

1
2
3
4
5
6
7
8
9
10
11
Input: Binary tree: [1,2,3,null,4]
       1
     /   \
    2     3
     \  
      4 

Output: "1(2()(4))(3)"

Explanation: Almost the same as the first example, 
except we can't omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.

题目解析

将树转化为字符串，如果节点的子树为空，就用()来替代，最后生成的字符串能省略的括号必须省略，但是省略不能引起歧义，比如第二个例子中，第一个()就不能省略。我是先序遍历，若左子树不为空，则先添加’(‘，再递归遍历root->left，然后添加’)’，如果左子树为空，根据右子树是否为空来判断是否加一个’()’，然后再遍历右子树，同样是先添加’(‘，再递归遍历右子树，然后添加’)’。但是效率很低，而且这个省略括号我想了挺久的。这样可以直接生成答案而不用再去精简。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    string res = "";
    string tree2str(TreeNode* t) {  
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        if(!t)
            return res;
        helper(t);
        return res;       
    }
    void helper(TreeNode* t){
        if(!t){
            return;
        }
        res = res + std::to_string(t->val);
        if(t->left){
            res += "(";
            helper(t->left);
            res += ")";
        }
        else{
            if(t->right)
                res += "()";
        }
        if(t->right){
            res += "(";
            helper(t->right);
            res += ")";    
        }
        return;            
    }
};

优化

看到一个runtime 4ms的答案，思路是一样的，但是它开始先加了一个’(‘，然后添加root->val。后面的思路是一样的，左子树为空且右子树不为空则添加’()’，然后递归遍历左子树和右子树，最后再加一个’)’，这样就相当于多加了一层括号，最后返回的时候进行了截断。开始我也在纠结这个是先加’(‘还是先加节点值，因为根节点左边是没有括号的，所以才有了后面繁琐的判断，这个优化的方案直接截断了，我怎么没想到呢，后面判断的逻辑简单了很多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    string tree2str(TreeNode* t) {
        if ( !t )  return "";
        string res = "";
        helper( t, res );
        return string( res.begin() + 1, res.end() - 1 );
    }
    
    void helper( TreeNode* t, string& res ) {
        if ( !t ) return;
        res += '(' + to_string( t->val );;
        if ( t->left == NULL && t->right ) {
            res += "()";
        }
        helper( t->left, res );
        helper( t->right, res );
        res += ')';
    }
};

993 Cousins in Binary Tree

题目描述

In a binary tree, the root node is at depth 0, and children of each depth k node are at depth k+1.

Two nodes of a binary tree are cousins if they have the same depth, but have different parents.

We are given the root of a binary tree with unique values, and the values x and y of two different nodes in the tree.

Return true if and only if the nodes corresponding to the values x and y are cousins.

题目解析

给定一棵二叉树和两个节点，判断两个节点是否是Cousins，就是深度一样，但是父节点不同。遍历二叉树，用一个变量保存深度，一个变量保存parent，最后比较深度和父节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    int x_level = -1,y_level = -1;
    int x_parent = -1,y_parent = -1;
    bool isCousins(TreeNode* root, int x, int y) {
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        if(!root)
            return false;
        int level = 0;
        helper(root,x,y,level,-1);
        //cout << x_level << ' ' << x_parent << endl;
        //cout << y_level << ' ' << y_parent << endl;
        if(x_level != y_level)
            return false;
        else{
            if(x_parent != y_parent)
                return true;
            else
                return false;
        }     
    }
    void helper(TreeNode *root, int x, int y, int level,int parent){
        if(!root)
            return;
        if(root->val == x){
            x_level = level; 
            x_parent = parent;
        }
        if(root->val == y){
            y_level = level;
            y_parent = parent;
        } 
        helper(root->left,x,y,level+1,root->val);
        helper(root->right,x,y,level+1,root->val);
        return;
    }
};

530 Minimum Absolute Difference in BST

题目描述

Given a binary search tree with non-negative values, find the minimum absolute difference between values of any two nodes.

Example:

1
2
3
4
5
6
7
8
9
10
Input:

   1
    \
     3
    /
   2

Output:
1

Explanation:
The minimum absolute difference is 1, which is the difference between 2 and 1 (or between 2 and 3).

题目解析

给定二叉搜索树，找出任意两个节点之间的最小绝对差。因为是二叉搜索树，所以中序遍历得到的正好是从小到大的顺序，一个元素的最小绝对差是与相邻的元素的绝对差。然后遍历求一个与相邻元素的差值，然后取最小值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:

    int getMinimumDifference(TreeNode* root) {
        ios::sync_with_stdio(0);
        cin.tie(0),cout.tie(0);
        if(!root)
            return 0;
        vector<int> vals;
        helper(root,vals);
        int res = abs(vals[1] - vals[0]);
        for(int i=1;i<vals.size()-1;i++){
            res = min(res,abs(vals[i+1]-vals[i]));
        }
        return res;

    }
    void helper(TreeNode* root, vector<int> &vals){
        if(!root)
            return;
        helper(root->left,vals);
        vals.push_back(root->val);
        helper(root->right,vals);
        return;
    }
};

100 Same Tree

题目描述

Given two binary trees, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical and the nodes have the same value.
Example 1:

1
2
3
4
5
6
7
Input:     1         1
          / \       / \
         2   3     2   3

        [1,2,3],   [1,2,3]

Output: true

Example 2:

1
2
3
4
5
6
7
Input:     1         1
          /           \
         2             2

        [1,2],     [1,null,2]

Output: false

Example 3:

1
2
3
4
5
6
7
Input:     1         1
          / \       / \
         2   1     1   2

        [1,2,1],   [1,1,2]

Output: false

题目解析

比较两棵树是否相同，只有结构和对应节点值相同，两棵树才叫做相同。学习到的就是该用else if的时候就要用，不要一堆的if，感觉逻辑和别人是一样的，但是效率就是低。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p==NULL && q==NULL)
            return true;
        else if((p==NULL && q!=NULL) ||(p!=NULL && q==NULL))
            return false;
        else if(p->val != q->val)
            return false;
        return (isSameTree(p->left,q->left) && isSameTree(p->right,q->right));
        
    }
};

404 Sum of Left Leaves

题目描述

Find the sum of all left leaves in a given binary tree.

Example:

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.

题目解析

求树的左叶子节点的节点值之和，可以用flag标记是否是左子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int sum = 0;
    int sumOfLeftLeaves(TreeNode* root) {
        if(!root)
            return 0;
        int flag = 0;
        helper(root,flag);
        return sum;
    }
    void helper(TreeNode* root, int flag){
        if(!root)
            return;
        if(root->right==NULL && root->left == NULL && flag == 1){
            sum += root->val;
            return;
        }
        helper(root->left,1);
        helper(root->right,0);
        return;
    }
};